4-1. 和差算

(Rev.0.00：2020/2/25)

こんにちは、kaneQです

「算数は図で考える」を身につけ、算数の成績を伸ばしましょう

参考：目次

今回から特殊算の分類ごとに「算数は図で考える」を実践します
本サイトでは、「基本」で説明した『問題文を、先頭から順に、そのまま図に書く』を中心に紹介しますが 、中には「応用」で説明したようにそのまま図に書けないような問題も扱う事があります。応用問題や発展問題の足掛かりと考えて是非、挑戦してみて下さい

今回のゴールは以下です
ゴール：「和差算」を線分図で解いてみる

和差算とは、２つの数量の和と差が与えられた場合のそれぞえの数量を求める問題です。数量は２つとは限らず３つやそれ以上の事もあります

本記事では以下の４つの問題を解いてみましょう

問題１（基本）

餃子が３０個あります。兄は弟より４個多く食べました。弟は餃子を何個食べたでしょう？

問題２（基本）

大、中、小３つの数があります。全部の合計は３５０です。大は中より２６大きく、中は小より１２大きいです。大、中、小の数はそれぞれいくつでしょう？ 

問題３（応用）

大、中、小３つの正方形がならんでいます。大、中、小のそれぞれの正方形の１辺の辺の長さはいくつでしょう？

問題４（応用）

ある船が川を上るときの速さは時速２０㎞で、同じ川を下るときの速さは時速２６㎞でした。この船の静水時の速さと川の流れの速さはそれぞれ時速何㎞でしょう。

問題１と問題２は２つの数量の和と差に関する条件がそのまま与えられている基本問題です。問題３と問題４は和と差がそのまま与えられているわけではないので応用問題になります

まずは自分で考え、考えてから答えを読んでください。答えと別の解き方をしても問題ありません

問題１（基本：数量の和と差に関する条件がそのまま与えられている）

餃子が３０個あります。兄は弟より４個多く食べました。弟は餃子を何個食べたでしょう？

いつものとおり、問題文をそのまま図に書きます。今回は兄と弟を比較したいので兄と弟を別の線であらわしてみます

この図から分かることはなんでしょう？ここが重要なのでよく考えてください

そうです。赤く囲った部分が２６個であることが分かります。赤くかこった部分は弟が食べた餃子の数が２つ分なので、弟が食べた餃子の数は

２６÷２＝１３

となり、１３個食べたことが分かります。これが答えです

（別解）兄が食べた個数を先に求める方法

兄が食べた個数を先に求める場合、次の図のように弟の線の長さを兄の線の長さにそろえてみます

弟の線を４個分伸ばすことになるので、合計は

３０＋４＝３４

となり３４個であることが分かります。この３４個は兄が食べた個数の２つ分なので、兄が食べた餃子の数は

３４÷２＝１７
となり１７個であることが分かります。兄は弟より４個多く食べているので弟が食べた餃子の数は

１７－４＝１３

となり１３個である事が分かります。これが答えです

問題２（基本：数量の和と差に関する条件がそのまま与えられている）

大、中、小３つの数があります。全部の合計は３５０です。大は中より２６大きく、中は小より１２大きいです。大、中、小の数はそれぞれいくつでしょう？ 

大/中/小の３つの数の合計と、大/中の差、中/小の差が示されています。大、中、小を比較するために３本の線であらわしてみます

このように書くと大、中、小の大きさの違いが分かりやすくなりますね。ここで、小を基準に中と大を考えてみます。小を基準にするので小の大きさの赤枠で囲うと以下のようになります

赤枠で囲った部分の数量は３００になります。これは小が３つ分の量なので、小は

３００÷３＝１００（小）

と求まります。中は小より１２大きいので

１００＋１２＝１１２（中）

と求まります。同じように、大は中より２６大きいので

１１２＋２６＝１３８（大）

となります。以上より、大、中、小はそれぞれ１３８、１１２、１００と求まりました

問題３（応用：数量の和と差に関する条件がそのまま与えられていない）

大、中、小３つの正方形がならんでいます。大、中、小のそれぞれの正方形の１辺の辺の長さはいくつでしょう？

この問題、どのように解くかわかりますか？

よく考えてみて下さい。大と中と小の３つの量があり、大/中/小の合計と、大/中の差、中/小の差が示されています。大、中、小を比較するために３本の線であらわしてみます

このように書くと大、中、小の大きさの違いが分かり安くなりますね。ここで、小を基準に中と大を考えてみます。小を基準にするので小の大きさの赤枠で囲うと以下のようになります

赤枠で囲った部分の数量は３００ｃｍになります。これは小が３つ分の量なので、小は

３００÷３＝１００（小）

と求まります。中は小より１２ｃｍ大きいので

１００＋１２＝１１２（中）

と求まります。同じように、大は中より２６ｃｍ大きいので

１１２＋２６＝１３８（大）

となります。以上より、大、中、小はそれぞれ１３８ｃｍ、１１２ｃｍ、１００ｃｍと求まりました

考え方は問題２と全く同じです。問題２と問題３は問題の出しかたが違いますが全く同じ問題です。算数は初めてみるような問題も、柔軟に考える事が大事です。問題３の場合、問題で与えられた図をただながめていても解き方がひらめかないかもしれません。線分図等、自分で図を書くクセをつけてみると良いでしょう

問題４（応用：数量の和と差に関する条件がそのまま与えられていない）

ある船が川を上るときの速さは時速２０㎞で、同じ川を下るときの速さは時速２６㎞でした。この船の静水時の速さと川の流れの速さはそれぞれ時速何㎞でしょう。

この問題は以下の前提知識が必要になります。

• 船が川を下る速さ＝船の静水時の速さ＋川の流れの速さ　・・・①
• 船が川を上がる速さ＝船の静水時の速さー川の流れの速さ　・・・②

この前提を理解した上で考えてみて下さい

そうです、「静水時の船の速さ」と「川の流れの速さ」の合計が上の①の条件であり、「静水時の船の速さ」と「川の流れの速さ」の差が②の条件である事に気づくと思います。ここで、「静水時の船の速さ」と「川の流れの速さ」をそれぞれ線であらわすとこのようになります

まずは、「川の流れの速さ」を考えてみます。「川の流れの速さ」を基準に赤枠で囲うと以下のようになります

赤枠で囲った部分の数量は６㎞になりますね。赤枠で囲った部分の数量は「川の流れの速さ」の２つ分なので

（川の流れの速さ）＝６÷２＝３（㎞）

とわかります。この事から静水時の船の速さは

（静水時の船の速さ）＝３＋２０＝２３（㎞）

と求めることができます。以上です

この問題は、「船が川を上るときの速さ」「船が川を下るときの速さ」を「静水時の船の速さ」と「川の流れの速さ」に分けて考える点がポイントです。「静水時の船の速さ」と「川の流れの速さ」に分けて考えることができれば和と差の関係から基本的な線分図を用いて解く事ができるのです

なお、この問題は「流水算」と考える事もできます。「流水算」では別の切り口で線分図を書く事もあります。別の線分図の書き方は、「流水算」に取り組むときに紹介します

以前も言いましたが、図の書き方は１通りではありません。何通りも書くことができます。自分独自の図の書き方であっても良いのです。１つのやり方にこだわらず柔軟に考える力を身につけていきましょう！

参考：目次

3-4-2. 線分図 - 応用２ -

[Rev.0.00 2020/2/9]

こんにちは、kaneQです

「算数は図で考える」を身に着け、算数の成績を伸ばしましょう

参考：目次

「線分図」について応用的な知識を身につける勉強の２回目です
今までは「問題文」をそのまま図に書くという基本方針で勉強を進めてきました。この考え方は今後も変わりませんが、「問題文に書いていない事も図に書き加える」事をしないと解けない問題があります
今回は、
「問題文で与えられていない基準を探し、数量を自分で設定して整理する」
という方法を紹介します。今後、基本問題であっても難易度が高い問題や応用問題、発展問題、難問と言われる問題を考える際に必須になっていく考え方です。頑張って身につけて下さい

今回のゴールは以下です

ゴール：基準とする数量を見つけ整理する事例を知る
(まずは知ってもらえれば良いです。身につけるための演習は別に用意します)

今回扱う問題は以下です。ニュートン算とよばれる問題で、基本問題としては難易度が少し高めです

ある水そうに一定の割合で水が流入し続け水があふれています。この水そうから４台のポンプで水をくみ出すと２４時間で水そうは空になり、６台のポンプでくみ出すと８時間で水そうは空になります。５台のポンプで水をくみ出すと、何時間で水そうは空になるでしょうか ？

まずは自分で考えてみて下さい

どうでしょうか？ノーヒントで解ければ本サイトの線分図は卒業です

まず、「はじめに水そうに入っていた水の量」を線分図として書きます

「４台のポンプで水をくみ出すと２４時間で水そうは空になり」とあるので２４時間で流入 する水の量を書き足します

この全体が「４台のポンプが２４時間にくみ出す水の量」なのでこのようになります

同様に「６台のポンプが８時間にくみ出す水の量」を書いて先ほどの図と並べるとこのよう になります

これだけだと解が進みません。ここでポイントです。問題文には書かれていませんが、１台のポンプがくみ出す量を①と設定してみます（★）

すると、「４台のポンプが２４時間にくみ出す水の量」「６台のポンプが８時間にくみ出す水の量」はそれぞれこのようになります

どうでしょうか？何か見えてきませんか？

そうです。いつもと同じく線をそろえると、差分として「16時間に流入する水の量は」

という事が分かります。よって
（１時間に流入する水の量）＝ ㊽ ÷１６＝③
という事が分かりました。つまり｢１時間に流入する水の量は３台のポンプが１時間にくみ出す水の量と同じ｣という事がわかりましたか。この事をもとに考えると・・・

２４時間に流入する量が

であり、はじめ水そうに入っていた水の量が

である事がわかりました

次に５台のポンプで水をくみ出す事を考えます。先ほど｢１時間に流入する水の量は３台のポンプが１時間にくみ出す水の量と同じ｣ということが明らかになりました。１時間に流入する水の量は③、５台のポンプがくみ出す水の量は⑤なので、⑤ － ③ ＝ ② から１時間に水は②減る事がわかります。

はじめ水そうに入っていた水の量は㉔でしたね。ですので㉔の水を５台のポンプを使うと

㉔ ÷ ② ＝ １２

つまり１２時間で空になることがわかりました。これで完了です

なお、５台のポンプを使う場合の計算は以下のように線分図と方程式を使って解くこともできます。理解できるようであれば、この解き方も身に付けると良いでしょう。

まず、５台のポンプを使う場合を図に書いてみましょう。「５台のポンプで水をくみ出すと□ 時間で水そうが空になる」を図にするとこのようになります

よって、
㉔ ＋ ③ × □ ＝ ⑤ × □　(一元一次方程式)
整理すると
② × □ ＝ ㉔
よって、
□ ＝ １２時間
という事が分かりました

以上です。今回の解法のポイントは

１台のポンプがくみ出す量を①と設定している(★)
です。これが、今回のゴールである「基準とする数量を見つけ整理する」です

このポイントを用いる必要があるため難易度が上がっていると思います。いうまでもないですが非常に重要な考え方です。今後、慣れていきましょう

ところで、今回「１台のポンプがくみ出す量を①」と設定しました。「基準とする数量を見つけ整理する」はわかっていない数量を設定するようにして下さい。今回は「１台のポンプがくみ出す量を①」としましたが、実は「１時間に流入する水の量を①とする」としてもこの問題は解く事ができます。問題文をよく読んで「わかっていない量」を見つけて基準とするという考え方を心がけて下さい。ここ、非常に大事ですよ

なお、今回は線分図を使って解きましたが、面積図を使うともう少し簡単に解けます

面積図を使った解き方はそのうち解説します。興味がある人はこまめにチェックしてみて下さい

どうですか？ 今回の内容は理解できたでしょうか？
本記事の内容は重要です。ですが、１問だけでは理解できないと思います。今後の演習問題で何度かでてきますのでだんだんと慣れていくと良いでしょう

それではまた！

参考：目次

方程式は使ってはいけないのか？

こんにちはkaneqQです

今回は、算数の勉強から少しはなれ問題を解くための立ち位置の確認をしたいと思います。具体的には、本サイトにおける方程式の扱いをある程度明確にしておこうと思います。いつもの勉強ではないので読み飛ばしてくれて大丈夫です。また、内容も難しいので理解できなくても問題ないです

よく、中学受験算数では｢方程式を使ってはいけない｣｢方程式は使うべきではない｣という記事を目にします

では実際にはどうなのでしょうか？
と問題提起しましたが、、、　この議論はよその記事におまかせします。すみませんm(__)m

私は
｢自分が自然に理解できる範囲でなら積極的に使うべき｣
と考えてます。方程式の考え方を使わないと説明が難しい解法がたくさんあるのです
例えばつるかめ算を面積図という解法で解く場合、本記事に掲載した問４の解２は方程式を利用する事で簡単に解くことができています
本サイトでは方程式を使った方が自然な場合には方程式（または方程式もどき）を使いますので、その点を理解しておいてもらえるとうれしいです

ただ、本サイトで扱う方程式（または方程式もどき）は一元方程式までにとどめるつもりです

以下では方程式の使用例をいくつか紹介しておきます。本サイトでは問４の解３くらいまでの考え方は使う事があります。問４の解４は使いません
（ちなみに、問４に関しては解２を使用するのが圧倒的に早く解けるので解２をお勧めします）

問１：イチゴが１０個あります。何個か食べたら４個残りました。何個食べましたか？

食べた数を□個とすると
１０ ー □ ＝ ４ (一元一次方程式)
が成り立ちます。よって
□ ＝ １０ ー ４ = ６
となり、食べた数は６個とわかります。実際にはこのように式を書く人は少ないと思いますが、頭のなかでは「１０ ー ４」を考えているはずです

問２：２５平方センチメートルの正方形があります。この正方形の一辺の長さは何センチメートルですか？

一辺の長さを□センチメートルとすると以下の式が成り立ちます。
□ × □ ＝ ２５ (一元二次方程式もどき)
この式で□に１、２、３・・・と当てはめていくと
□ ＝ ５
である事がわかります。よって、一辺の長さは５センチメートルとなります
なお、上記を一元二次方程式と言ってしまうと
□ = ５ または －５
となります。しかし、ここでは「－５」は考えない事にします。よって、「もどき」という表現を使わせてもらいました

問３：１２５立方センチメートルの立方体があります。この立方体の一辺の長さは何センチメートルですか？

一辺の長さを□センチメートルとすると以下の式が成り立ちます
□ × □ × □ ＝ １２５ (一元三次方程式)
この式で□に１、２、３・・・と当てはめていくと
□ = ５
である事がわかります。よって、一辺の長さは５センチメートルとなります

問４：鶴と亀があわせて１５匹います。足の数はあわせて４０本です。亀は何匹いますか？

（解１）
すべて鶴とすると足の数は
２×１５＝ ３０
で１０本足りませんね。亀が１匹増えると
２×１４ ＋ ４ × １＝ ３２
で足の数の合計が２増えます。
４０ － ３０ ＝ １０
なので足の数の合計を１０増やすために亀を□匹と考えると
２ × □ ＝ １０（一元一次方程式）
となり
□ ＝ ５
となり亀は５匹ということがわかります

（解２）
面積図を使う方法

全体の足の本数は青枠で囲った部分の面積と考えると４０です
この図で赤枠でかこった部分の面積は
２×１５＝ ３０
となり、よってオレンジ色の枠で囲った部分の面積は
４０ － ３０ ＝ １０
となります。ここで亀の数を□匹とすると
２× □ ＝ １０（一元一次方程式）
が成り立ちます。よって、
□ ＝ ５
となるので亀は５匹ということがわかります

（解３）
面積図を参考に亀の数を□として式に落とし込む方法

４ × □ ＋ ２ × ( １５－ □ ) ＝ ４０（一元一次方程式）
この式を展開すると以下のようになります
４ × □ ＋ ３０ － ２ × □ ＝ ４０
この式を整理すると
２ × □ ＝ １０
となり、
□ ＝ ５
と求まります。よって亀は５匹という事が分かりました

（解４）
面積図を参考に鶴の数をx、亀の数をyとして式に落とし込む方法

鶴の足は２本で、亀の足は４本で足の数の合計が４０なので
２ × x ＋ ４ × y ＝ ４０・・・①（二元一次方程式）
が成り立ちます。また、鶴と亀をあわせると１５匹なので、
x ＋ y ＝ １５・・・②（二元一次方程式）
が成り立ちます。①、②をあわせるといわゆる連立方程式となります
②の式を変形すると
x ＝ １５－ y
となり、このｘを①の式のｘに代入すると
２× ( １５ － y ) ＋ ４ × y ＝ ４０
となります。この式を整理すると
３０ － ２ × y ＋ ４ × y ＝ ４０
となり、さらに整理すると
２ × y = １０
となり、最終的に
y = ５
となります。よって、亀は５匹という事が分かりました

おそらく世の中の｢方程式を使ってはいけない｣｢方程式は使うべきではない｣という意見の大半は連立方程式の事を指していると思われます
上記例の問１から問４の解２くらいのレベルは使っても弊害はないのです

如何でしょうか？

 [Rev.0.00 2020/2/3]

3-4-1. 線分図 - 応用 -

[Rev.0.00 2020/2/1]

こんにちは、kaneQです

「算数は図で考える」を身に着け、算数の成績を伸ばしましょう

参考：目次

「線分図」の標準に引き続き、応用的な知識を身につけていきましょう

線分図を使って解く問題の多くは、入門、基本、標準までの知識で解く事ができます。しかし、標準までの知識では対応できない問題があるのも事実です。そのような応用的な問題を何回かに分けて紹介したいと思います

今回は、いっけん線分図では解けないと思える問題を、線分図で解く方法を紹介します。考え方の分類としては、「基本」で紹介した「そろえる」という手法です。しかし、今回紹介する方法は知っていなければ使えないテクニックです。頑張って身につけて下さい

「応用」のゴールは以下です

ゴール１：比をそろえるテクニックを身につける

ゴール２：比例式に挑戦してみる

今回扱う問題は以下の２つです。まずは自分で考えてみて下さい

太郎と次郎が持っているお金の比は７：２でした。その後太郎は５００円使い、次郎は１０００円もらったので、２人のお金の比は３：２になりました。
今、次郎は何円持っているでしょうか？

今まで学んできたように、問題文をそのまま図に書きましょう。「太郎と次郎が持っているお金の比は７：２でした」はこのようになりますね

次に、「その後太郎は５００円使い、次郎は１０００円もらった」「２人のお金の比は３：２になりました」を書き足すとこうなります

どうでしょうか。この図から何か分かるでしょうか？
残念ながら、このままでは答えに結びつく考えはうかびません(実は、この図から比例式をたてて解く方法があります。比例式を使って解く方法は後述します)

ではどうすれば良いでしょうか。実は、考え方としては「基本」で紹介した「そろえる」を当てはめるとそろえたところとの差分が明確になります
今回は、「比の大きさをそろえる」というテクニックを使います。ここで比とは○で囲った数字、または、□でかこった数字です。○か□のどちらかを「そろえます」。そろえるのはどちらでもよいですが、今回は□でかこった数字をそろえてみましょう

太郎の線分図では□３、次郎の線分図では□２ですね。これを３と２の最小公倍数の６の大きさにそろえてみましょう。そのためには太郎の線分図を２倍の長さに伸ばし、次郎の線分図を３倍の長さに伸ばせばよいですね。すると、こうなります

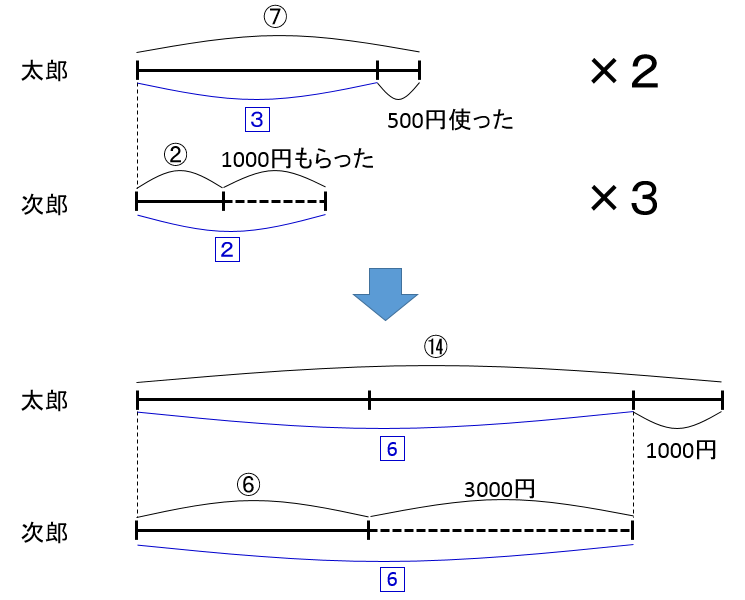
□で囲った□６の長さで図がそろいました。さあ、何か見えてきませんか？

そうです。赤字で書いた部分が差として明確になってきました。赤い部分を比の大きさであらわすと
⑭ - ⑥ = ⑧
となります。一方で金額であらわすと
3000円＋1000円 = 4000円
となります。つまり、比の大きさと金額を式に当てはめると
⑧ = 4000円
となりますね？よって、
① = 500円
を導くことができました。元の図では次郎は
② + 1000円
持っていることが分かります。よって、
② + 1000 = ① × 2 + 1000 = 500 × 2 + 1000 = 2000円
という事が分かりました

どうですか？「そろえる」という考え方を応用する事で、いっけん線分図では解けないと思える問題も解く事ができました

このような考え方は算数のネタとしては非常に面白いと言えるでしょう
ただ、この解き方は線分図に固執した特殊な考え方のようにも思えます。線分の比をそろえるためにそれぞれを伸ばすという事の意味というか本質というかを小学生で理解するのは非常に難しいと思います。難関校に受かるレベルの子であってもほとんど理解できていないのではないかと思います。そう考えると、この解き方は解くためのテクニックに過ぎないと言えるかもしれません。冒頭で｢知っていなければ使えないテクニック｣と紹介したのはそのためです

解き方を暗記する事は百害あって一利なしと言われています。。。 ですが、この比をそろえるテクニックは覚えておいた方が良いです

さて、今回の問題は特殊算の分類的には「倍数変化算」に分類することができます

倍数変化算は比例式というもので簡単に解く事ができます。以下では、別解として、比例算で解く方法を紹介します

(別解)
問題図をそのまま図に書くところまでは同じです。「太郎と次郎が持っているお金の比は７：２でした」「その後太郎は５００円使い、次郎は１０００円もらった」「２人のお金の比は３：２になりました」を書き足すとこうなります(上でも同じ図を書きました)

この図を比例式で書くにはどうすれば良いでしょうか。難しくはありません。そのまま素直に考えてみましょう

まず、太郎については○７持っていた状態から５００円使って□３の比になります。次に、次郎は○２持っていた状態から１０００円もらって□の２の比になります。これを比例式の形式で書くだけです。こうなります

(⑦ - 500)：(② + 1000) = 3 : 2
比例式では内項の積と外項の積は等しいので
(⑦ - 500) × 2=(② + 1000) × 3

これを整理すると
⑭ - 1000 = ⑥ + 3000

こうなります。さらに整理すると
⑧ = 4000

こうなります。つまり
① = 500

となります。次郎は
② + 1000円
持っているので
② + 1000 = ① × 2 + 1000 = 500 × 2 + 1000 = 2000円
となります。

この、別解の解き方は、問題文を図に書くまではいつもと同じです。しかし図に書いて問題文を整理した後は式に置き換えて解くいう点が今までにない解き方と言えるでしょう

なお、比例式は、図を書かなくても問題文から直接導く事もできます。しかし、少し複雑になってくると頭の中だけでは整理するのが難しくなります。必ず図を書くようにしましょうね

比例式は方程式と同じく中学受験算数の世界では反対意見もありますが、私としては倍数変化算は比例式で考えるのが自然と思ってます。比の長さをそろえて解く方法よりも分かり易く間違いも少なくなります

是非、使いこなせるようになりましょう！

もう一問挑戦してください。同じく倍数変化算です。年齢算でもあります

母、花子さん、弟がいます。母の年齢は弟の７倍です。弟は花子さんより４才年下で、今から２年前、母の年齢は花子さんの年齢の５倍でした。

今、花子さんは何才ですか？

いつものとおり、問題文をそのまま図に書いてみましょう

「４才」や「２年」等の具体的な数量が示されている母と花子に着目してみましょう。何か分かるでしょうか？

先ほどと同様にまだ何もわからないと思います

今回も、「比の大きさをそろえる」というテクニックを使ってみましょう。○で囲った数字、または、□でかこった数字のどちらかをそろえてみます。□を５にそろえるのが一番簡単そうですね。このようになります

ここまで来るといつものとおり見えてくるものがあります。そうです

⑦ - ⑤ = 10年 + 2年

よって、② = 12年

よって、①＝６年

元の図で考えると弟が①なので６才ですね。花子は弟より４才年上なので１０才となります

さて、この問題も比例式で解く事ができます。以下、比例式を用いた別解です

(別解)

いつものとおり、問題文をそのまま図に書いてみましょう

母と花子さんを比例式で書くとこうなります

( ⑦ - 2 ) ： ( ① + 2 ) = 5：1

よって、

( ⑦ - 2 ) × 1 = ( ① + 2 ) × 5

よって、

⑦ - ⑤ = 10 + 2

よって、

② = 12

よって、

① = 6

よって、弟は６才、花子は弟より４才年上なので１０才となります

どうでしたでしょうか？

ゴール１：比をそろえるテクニックを身につける

ゴール２：比例式に挑戦してみる

は達成できたでしょうか。本記事の内容は重要です。理解できるまで、ぜひとも、何度も読んでみて下さい

それではまた！

参考：目次

3-3. 線分図 - 標準 -

[Rev.1.01 2020/1/9]

こんにちは、kaneQです

「算数は図で考える」を身に着け、算数の成績を伸ばしましょう

参考：目次

「線分図」の基本に引き続き、標準的な知識を身につけていきましょう
標準的な知識を身につける事で応用問題、発展問題、難問への足掛かりが整います

「標準」のゴールは以下です

ゴール：比を使った線分図を理解する

今回扱う問題は以下の２つです。まずは自分で考えてみて下さい

【問１】

今、たろう君とお父さんの年れいの和は５０才です。お父さんの年れいはたろうくんの年れいの４倍です。今のたろう君とお父さんはそれぞれ何才でしょう。

【問２】

今、たろう君は１０才でお父さんは４０才です。お父さんの年れいがたろう君の年れいの３倍になるのは何年後でしょう。

最後まで解けなくても良いです。

書けるところまで図を書いてみて下さい

それでは問題１からやっていきましょう

【問１】

今、たろう君とお父さんの年れいの和は５０才です。お父さんの年れいはたろうくんの年れいの４倍です。今のたろう君とお父さんはそれぞれ何才でしょう。

二人の年齢を比較すると分かりやすそうなので、２本の線分図にしてみます

１本の線分図で解いてみたい人は、ぜひ一本の線分図でやってみて下さい。この問題は一本の線分図でも充分にとけます

まず｢たろう君とお父さんの年れいの和は５０才です｣を線であらわしてみましょう

ここまでは大丈夫と思います。ただそのまま書けば良いです。ただし、線の書きはじめはそろえましょう

次に「お父さんの年れいはたろうくんの年れいの４倍です」を書き足してみます

ここで注意。線分図(や面積図などの図)に割合や比を書くときは普通の数量と違うので、単なる数字ではなく、丸や三角などでくるんだ数字を書くと区別がつきやすくなります

上の図では「４倍」を表すために数字の４を丸でかこってみました。たろう君が①なのに対して、お父さんが④なので「お父さんの年れいはたろうくんの年れいの４倍です」を表すことができましたね！

さあ、気づくことがあるでしょうか？

そうです。たろう君の①とお父さんの④をあわせると⑤になり、あわせた⑤が５０才です。つまり

　⑤＝５０才

が成り立ちますね。なので、⑤を５でわると①になり

　①＝５０÷５＝１０才

となります。よって、たろう君は１０才です。そしてお父さんは④なので

　④＝１０×４＝４０才

となります。たろう君とお父さんを足すと１０＋４０＝５０才になります。また、お父さん（４０才）はたろう君（１０才）の４倍ですね。よって、問題の条件とあった事が確認できました。これで正解です！

【問２】

今、たろう君は１０才でお父さんは４０才です。お父さんの年れいがたろう君の年れいの３倍になるのは何年後でしょう。

二人の年齢を比較すると分かりやすそうなので、２本の線分図にしてみます

まず「たろう君は１０才でお父さんは４０才です」を線であらわしてみましょう

次に、「お父さんの年れいがたろう君の年れいの３倍になるのは何年後」を書き足してみます。何年後かを□であらわして□の分線を伸ばします

ここでは、たろう君とお父さん両方が同じ□伸びる事になります。差はそろえた方と逆側にあらわしていますが、□分伸ばすのはそろえた側にしましょう。こうする事で差が分かりやすいままになります

この図を見て何か分かってくる事はありませんか。まずは一人で考えてみて下さい

（まだ下の説明には進まないでください）

分かったでしょうか？

分かりやすいように青い線を書き足して長さをそろえてみます。長さをそろえた部分に太朗君とお父さんの年の差と比の差を書いてみます。

たろう君とお父さんの年の差は３０才ですね。また、たろう君とお父さんの年の比の差は②になります

②＝３０才という事が分かりますね。だから①は３０÷２で１５才となります

たろう君の線の①の部分が１５才なので、□は１５－１０で５。つまり5年後となります

問１も問２も比を使って解く問題です。線分図を書く事で比の大きさと実際の数量の関係がわかってきます。そして比の大きさと数量の関係を用いて答えを導いていく事になります

比を使う事で線分図の世界が広がります！

 それでは、楽しんでいきましょう！

参考：目次

3-2. 線分図 - 基本 -

[Rev.1.04 2020/4/8]

こんにちは、kaneQです

「算数は図で考える」を身につけ、算数の成績を伸ばしましょう

参考：目次

前回は「入門」として「問題文をそのまま線分図に書く感覚を身につける」に取り組みました
本記事では、「基本」として問題を解くうえで押さえておくべき事を紹介します

「基本」のゴールは以下です
ゴール：図を使って問題を解く場合のポイントを理解する

【問１】
赤と青のリボンがあわせて１５mあります。青いリボンは赤いリボンより3m長いそうです。赤と青のリボンはそれぞれ何ｍですか？

前回紹介した問題です。もう一度考えてみましょう。前回は以下のような線分図を書きました

【問１の解１】

これも間違いではありません。ですが、問１をもう少し複雑にした問２を1本の線分図で書くとどうなるでしょうか？

【問２】

赤と青と黄のリボンがあわせて１５ｍあります。青いリボンは赤いリボンより３ｍ長いそうです。黄色いリボンは赤いリボンより６ｍ長いそうです。赤と青と黄色のリボンはそれぞれ何ｍですか？

問１と同じように１本の線分図で書くと以下のようになります

 リボンの大小関係が分かりにくい図になってしまいました。リボンの数が４本や５本になると、１本の線分図を使って問題を整理する事が困難になります

このようなときは図を分けて考えると分かりやすくなります

図を分けるとはどういうことか、問１に戻って考えてみましょう

今回の問題は赤いリボンと青いリボンの長さを考える問題です。このようにいくつかの数量を比べるときは、比べるものの図を分けて考えると分かりやすくなります

赤いリボンと青いリボンをわけて書いていきましょう

 【問１】
赤と青のリボンがあわせて１５mあります。青いリボンは赤いリボンより3m長いそうです。赤と青のリボンはそれぞれ何ｍですか？

【問１の解２】

「赤と青のリボンがあわせて１５mあります」をそのまま線分図に書きます。問１の解１の時と違うのは分けて図を書いている点です

次に、「青いリボンは赤いリボンより3m長いそうです」を書き足してみます

何か見えてきませんか？

青い点線でかこった部分が赤いリボン2本分ということに気付いてください。全体から３m短い長さが赤いリボン２本分ということになりますね。

青い点線でかこった部分全部の長さは

１５－３＝１２（ｍ）

赤いリボンの長さはその半分なので

１２÷２＝６（ｍ）

となります。青いリボンは

６＋３＝９（ｍ）

となります

図を分けて考える事で問題を解く事ができました

ところで、この図には重要なポイントが隠されている事に気づいたでしょうか？

算数が得意な子は無意識でできている事ですが、算数が苦手！図が書けない！図を書いても解き方が分からない！という子はポイントを知らないのではないでしょうか

「なにやらたいそうな事を覚えないといけないようだ」と感じないでください。難しくありません。一体どういう内容でしょうか？今回書いた図を見直してみます

 何気なく図を書きましたが、「線のはしをそろえている」「そろえたほうと逆側で差をくらべている」となっています

問１を解くときに「青い点線でかこった部分が赤いリボン2本分」を強調しましたが、この点について、問１の解２をもう一度見てみてください

見ましたか？

では「線のはしをそろえる」「そろえたほうと逆側で差をくらべている」をしないとどうなるでしょうか。まず、「線のはしをそろえる」をしない場合を考えてみます

 線のはしをそろえずに書くとこのようになります。「青い点線でかこった部分が赤いリボン2本分」というような関係に気づくことが難しくなりました（というか気づけないと思います）

次に「そろえたほうと逆側で差をくらべている」をしない場合を考えてみます

 「そろえたほうと逆側で差をくらべている」をせずに、そろえたほうと同じ側に差を書きこむとこのようになります。こちらも「青い点線でかこった部分が赤いリボン2本分」というような関係に気づくことが難しくなりました（というか気づけないと思います）

以上より、「わける（図をわけて書く）」「そろえる」「差はそろえた方と逆側にかく」がポイントになります。ところで、「そろえる」にはもう一つ非常に重要な使い方があります

問１を別の解き方をし、その中でもう１つのポイントを紹介したいと思います

  【問１】
赤と青のリボンがあわせて１５mあります。青いリボンは赤いリボンより3m長いそうです。赤と青のリボンはそれぞれ何ｍですか？

【問１の解３】

 「赤と青のリボンがあわせて１５mあります」「青いリボンは赤いリボンより3m長い」を線分図に書くところまでは解２と同じです

次に、赤いリボンを伸ばして青いリボンと長さをそろえてみます

赤いリボンを３ｍのばして長さをそろえる事でこのようになりました。何か見えてきませんか？

青い点線でかこった部分が青いリボン2本分ということに気付いてください。全体から３m長い長さが青いリボン２本分ということになりますね。

青い点線でかこった部分全部の長さは

１５＋３＝１８（ｍ）

青いリボンの長さはその半分なので

１８÷２＝９（ｍ）

となります。赤いリボンは

９ー３＝６（ｍ）

となります

【問１】について、いろいろな図の書き方を見てきましたが、混乱するでしょうか？

図の書き方を覚えようとしないで下さいね。覚えようとすると混乱します。当然すべての図の解き方を覚える事はできません。意味もありません

実際には、初めて問題に向き合ったときにいきなり正解の図がかけるとは限りません。むしろ、正解の図が書けない事が多いはずです

 いきなり正解の図がかけない事は当たり前と思ってください。だれでもそうです

問題を見たらまずどんな図でもよいので手を動かしてみましょう。そしてうまく整理できなかったらすぐに別の図を書いてみましょう

別の図を書くときはわける、そろえるを意識しすると良いです。また、複数の線で線分図を書いてうまくいかないときには１本の線にしてみるというのも当然ありです

線分図以外の図をかいてみるのも良いです

正解図も１つではありません。今回の【問１】も

• １本の線で線分図を書く（解１）
• ２本の線で線分図を書く（解２）
• ２本の線で線分図を書く（解３）

を紹介しましたね。すべて正解なのです。他にも正解の図はいくらでもかけます

ここまで見てきた「算数は図で考える」のポイントをまとめます

問題を解くポイント

1.問題文を、先頭から順に、そのまま図に書く
2.図に書く事で見えてくる事を図に書き足していく
3.いつのまにか問題が解けている

こちらについては「２．事例紹介」で説明しました。気になる人はもう一度見てみて下さい

「そのまま図に書く」ときのポイント

数量を比べたり整理するために

1.わける

2.そろえる

　線分図の場合：線の書き出しをそろえる、線の長さをそろえる

3.差はそろえた方と逆側で考える

解く力を伸ばすためのポイント

1.とにかく図を書く（図を書いて書いて書きまくる）

2.書いた図が分かりにくかったらすぐに別の図を書く

　分ける、そろえるを使ってみる

　面積図等の他の表現方法をつかってみる

それでは、頑張りましょう！

参考：目次

3-1. 線分図 - 入門 -

[Rev.1.00 2019/11/26]

こんにちは、kaneQです

「算数は図で考える」を身に着け、算数の成績を伸ばしましょう

参考：目次

お待たせしました。ようやく基本からの学習をスタートします
まずは「線分図」から学びましょう

とりあえず、「入門」「基本」「標準」に分けて進めます。今回は「入門」です

「入門」のゴールは以下です

ゴール：問題文をそのまま線分図に書く感覚を身につける

【はじめに】
文章題を解くためには、何が必要でしょうか？
問題を解くために、足し算、引き算、かけ算、わり算、少数、分数、比、割合等の知識が必要になります

ですが、一番大事なのは「図を書く力」です。図を書く事で数量の関係を明確にし、解くための式が導けるようになります。算数が得意な子は、例外なく「図を書く力」が身についているのです

今回は、図の中でも避けて通ることはできず、また、極めて応用範囲の広い線分図を理解する事にします

【線分図とは】
ところで線分図って何でしょう？

線分図は、数量を線の長さを使って表した図の事です。線分図で扱う数量は、個数、年齢、 時間、日数等なんでもよいです
線分図＝数量を表す図
くらいに覚えておくと良いでしょう

算数の問題を解くときは、「問題文を、先頭から順に、そのまま図に書く」を意識してください。とはいえ、初めは、「そのまま図に書く」ができないかもしれません

本記事では入門編として、超簡単な問題から入っていきたいと思います。以下のそれぞれを線分図であらわしてみてください

【問１】
３＋４＝□

【問２】
７＋□＝１５

【問３】
１１ー□＝４

【問４】
赤と青のリボンがあわせて１５mあります

【問５】
赤と青のリボンがあわせて１５mあります。青いリボンは赤いリボンより3m長いそうです

それでは順番にやってみましょう

【問１】
３＋４＝□

分かるでしょうか。難しく考える必要はありません。３という数、４という数を並べて書いてみましょう

これだけです。そして、３と４を足したのが□なので

このようになります。わざわざ図にするまでもないかもしれませんが、線分図ってこんなもんです

【問２】
７＋□＝１５

次はこれを線分図であらわしてみましょう。これも同じです。７という数と□という数を並べて書いてみましょう

これだけです。そして、７と□を足したのが１５なので

こうなります。図に書くと数量どうしの関係がよくわかるようになると思いませんか？

【問３】
１１ー□＝４

この問題は解けますか？３年生の前半くらいだと少し悩むかもしれません。１１という数から□を引くという内容の図を書いてみます

こうなります。そして、１１という数から□を引くと４になるのですから、図を書き足してみます

ここまで書くと、全体の関係がはっきりします。全体の関係がはっきりすると、□は１１から４を引いた数という事が理解できると思います

【問４】
赤と青のリボンがあわせて１５mあります

まず「赤と青のリボンが」を線分図にします

次に「あわせて１５ｍあります」をつけたしてみましょう

どうでしょうか。難しく考えないでくださいね。「問題文を、先頭から順に、そのまま図に書く」だけで良いのです

【問５】
赤と青のリボンがあわせて１５mあります。青いリボンは赤いリボンより3m長いそうです

これはどうでしょうか。少し悩んでしまうかもしれませんね。でも、難しく考えないで下さい。悩んでしまって手を止めてはいけませんよ。間違えてもいいからまずは「問題文を、先頭から順に、そのまま図に書く」をしてみましょう。書いてからおかしいなと思ったら書き直せばよいです

「赤と青のリボンがあわせて１５ｍあります」は問４と同じなのでこのようになります

そして、「青いリボンは赤いリボンより３ｍ長い」を書き足してみましょう

「青いリボンは赤いリボンより３ｍ長い」を図に書きこむとこのようになります

今回の「線分図 - 入門 -」ではここまでで終了です

今回の目的は「問題文をそのまま線分図に書く感覚を身につける」でした。「そのまま図に書く」ということはどういうことかわかったでしょうか

「そのまま図に書く」は訓練が必要です。すんなり身につけば良いです。そうでない人は、文章題に限らず１行問題等でも「図にかけるものはどんどん図を書く」という練習をしてみましょう

次回は、線分図から問題の答えを導く具体例の紹介ともう少し複雑な線分図の紹介をしたいと思います

【おまけ】

問５の続きですが、赤いリボンと青いリボンの長さは以下のように求めます 

赤いリボンと青いリボンをあわせると１５ｍですが、１５ｍから図の３ｍを引くと１２ｍになりますね。この１２ｍは赤いリボン２本分ですので、赤いリボンの長さは６ｍであることが分かります

そして、赤いリボンが６ｍとわかったら、青いリボンは赤いリボンよりも３ｍ長いので９ｍという事になります

なお、問５は「和差算」といわれる問題です。上で説明した線分図とは別の図の書き方もあります。次回、別の図の書き方を説明するので楽しみにしていてください

参考：目次