3-4-1. 線分図 - 応用 -

[Rev.0.00 2020/2/1]
こんにちは、kaneQです
「算数は図で考える」を身に着け、算数の成績を伸ばしましょう
参考:目次
「線分図」の標準に引き続き、応用的な知識を身につけていきましょう
線分図を使って解く問題の多くは、入門、基本、標準までの知識で解く事ができます。しかし、標準までの知識では対応できない問題があるのも事実です。そのような応用的な問題を何回かに分けて紹介したいと思います
今回は、いっけん線分図では解けないと思える問題を、線分図で解く方法を紹介します。考え方の分類としては、「基本」で紹介した「そろえる」という手法です。しかし、今回紹介する方法は知っていなければ使えないテクニックです。頑張って身につけて下さい
「応用」のゴールは以下です
ゴール1:比をそろえるテクニックを身につける
ゴール2:比例式に挑戦してみる
今回扱う問題は以下の2つです。まずは自分で考えてみて下さい
太郎と次郎が持っているお金の比は7:2でした。その後太郎は500円使い、次郎は1000円もらったので、2人のお金の比は3:2になりました。
今、次郎は何円持っているでしょうか?
今まで学んできたように、問題文をそのまま図に書きましょう。「太郎と次郎が持っているお金の比は7:2でした」はこのようになりますね

次に、「その後太郎は500円使い、次郎は1000円もらった」「2人のお金の比は3:2になりました」を書き足すとこうなります

どうでしょうか。この図から何か分かるでしょうか?
残念ながら、このままでは答えに結びつく考えはうかびません(実は、この図から比例式をたてて解く方法があります。比例式を使って解く方法は後述します)
ではどうすれば良いでしょうか。実は、考え方としては「基本」で紹介した「そろえる」を当てはめるとそろえたところとの差分が明確になります
今回は、「比の大きさをそろえる」というテクニックを使います。ここで比とは○で囲った数字、または、□でかこった数字です。○か□のどちらかを「そろえます」。そろえるのはどちらでもよいですが、今回は□でかこった数字をそろえてみましょう
太郎の線分図では□3、次郎の線分図では□2ですね。これを3と2の最小公倍数の6の大きさにそろえてみましょう。そのためには太郎の線分図を2倍の長さに伸ばし、次郎の線分図を3倍の長さに伸ばせばよいですね。すると、こうなります
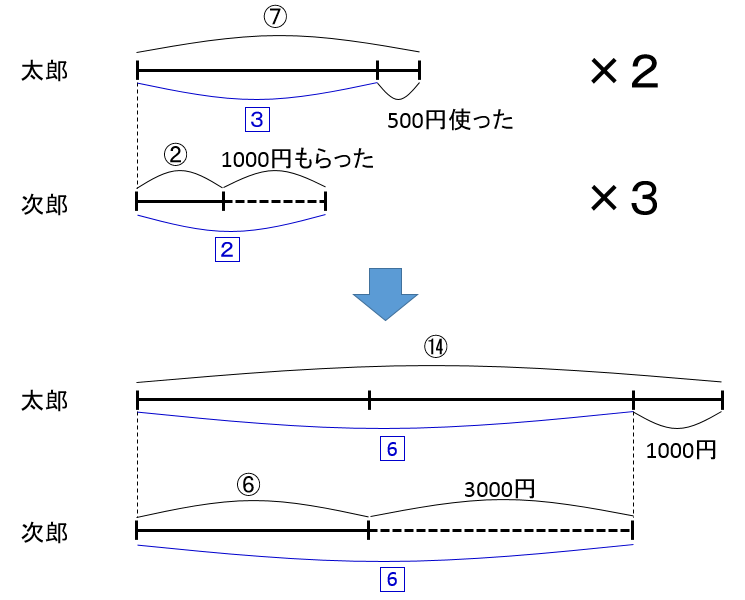
□で囲った□6の長さで図がそろいました。さあ、何か見えてきませんか?

そうです。赤字で書いた部分が差として明確になってきました。赤い部分を比の大きさであらわすと
⑭ - ⑥ = ⑧
となります。一方で金額であらわすと
3000円+1000円 = 4000円
となります。つまり、比の大きさと金額を式に当てはめると
⑧ = 4000円
となりますね?よって、
① = 500円
を導くことができました。元の図では次郎は
② + 1000円
持っていることが分かります。よって、
② + 1000 = ① × 2 + 1000 = 500 × 2 + 1000 = 2000円
という事が分かりました
どうですか?「そろえる」という考え方を応用する事で、いっけん線分図では解けないと思える問題も解く事ができました
このような考え方は算数のネタとしては非常に面白いと言えるでしょう
ただ、この解き方は線分図に固執した特殊な考え方のようにも思えます。線分の比をそろえるためにそれぞれを伸ばすという事の意味というか本質というかを小学生で理解するのは非常に難しいと思います。難関校に受かるレベルの子であってもほとんど理解できていないのではないかと思います。そう考えると、この解き方は解くためのテクニックに過ぎないと言えるかもしれません。冒頭で「知っていなければ使えないテクニック」と紹介したのはそのためです
解き方を暗記する事は百害あって一利なしと言われています。。。 ですが、この比をそろえるテクニックは覚えておいた方が良いです
さて、今回の問題は特殊算の分類的には「倍数変化算」に分類することができます
倍数変化算は比例式というもので簡単に解く事ができます。以下では、別解として、比例算で解く方法を紹介します
(別解)
問題図をそのまま図に書くところまでは同じです。「太郎と次郎が持っているお金の比は7:2でした」「その後太郎は500円使い、次郎は1000円もらった」「2人のお金の比は3:2になりました」を書き足すとこうなります(上でも同じ図を書きました)

この図を比例式で書くにはどうすれば良いでしょうか。難しくはありません。そのまま素直に考えてみましょう
まず、太郎については○7持っていた状態から500円使って□3の比になります。次に、次郎は○2持っていた状態から1000円もらって□の2の比になります。これを比例式の形式で書くだけです。こうなります
(⑦ - 500):(② + 1000) = 3 : 2
比例式では内項の積と外項の積は等しいので
(⑦ - 500) × 2=(② + 1000) × 3
これを整理すると
⑭ - 1000 = ⑥ + 3000
こうなります。さらに整理すると
⑧ = 4000
こうなります。つまり
① = 500
となります。次郎は
② + 1000円
持っているので
② + 1000 = ① × 2 + 1000 = 500 × 2 + 1000 = 2000円
となります。
この、別解の解き方は、問題文を図に書くまではいつもと同じです。しかし図に書いて問題文を整理した後は式に置き換えて解くいう点が今までにない解き方と言えるでしょう
なお、比例式は、図を書かなくても問題文から直接導く事もできます。しかし、少し複雑になってくると頭の中だけでは整理するのが難しくなります。必ず図を書くようにしましょうね
比例式は方程式と同じく中学受験算数の世界では反対意見もありますが、私としては倍数変化算は比例式で考えるのが自然と思ってます。比の長さをそろえて解く方法よりも分かり易く間違いも少なくなります
是非、使いこなせるようになりましょう!
もう一問挑戦してください。同じく倍数変化算です。年齢算でもあります
母、花子さん、弟がいます。母の年齢は弟の7倍です。弟は花子さんより4才年下で、今から2年前、母の年齢は花子さんの年齢の5倍でした。
今、花子さんは何才ですか?
いつものとおり、問題文をそのまま図に書いてみましょう

「4才」や「2年」等の具体的な数量が示されている母と花子に着目してみましょう。何か分かるでしょうか?
先ほどと同様にまだ何もわからないと思います
今回も、「比の大きさをそろえる」というテクニックを使ってみましょう。○で囲った数字、または、□でかこった数字のどちらかをそろえてみます。□を5にそろえるのが一番簡単そうですね。このようになります

ここまで来るといつものとおり見えてくるものがあります。そうです
⑦ - ⑤ = 10年 + 2年
よって、② = 12年
よって、①=6年
元の図で考えると弟が①なので6才ですね。花子は弟より4才年上なので10才となります
さて、この問題も比例式で解く事ができます。以下、比例式を用いた別解です
(別解)
いつものとおり、問題文をそのまま図に書いてみましょう

母と花子さんを比例式で書くとこうなります
( ⑦ - 2 ) : ( ① + 2 ) = 5:1
よって、
( ⑦ - 2 ) × 1 = ( ① + 2 ) × 5
よって、
⑦ - ⑤ = 10 + 2
よって、
② = 12
よって、
① = 6
よって、弟は6才、花子は弟より4才年上なので10才となります
どうでしたでしょうか?
ゴール1:比をそろえるテクニックを身につける
ゴール2:比例式に挑戦してみる
は達成できたでしょうか。本記事の内容は重要です。理解できるまで、ぜひとも、何度も読んでみて下さい
それではまた!
参考:目次